There is a golden rule in Machine Learning that states: the more data, the better. This rule is a double-edged sword. An indiscriminate addition of data might introduce noise, reduce model performance, and slow down its training process. In this case, more data can hurt model performance, so it’s essential to understand how to deal with it.
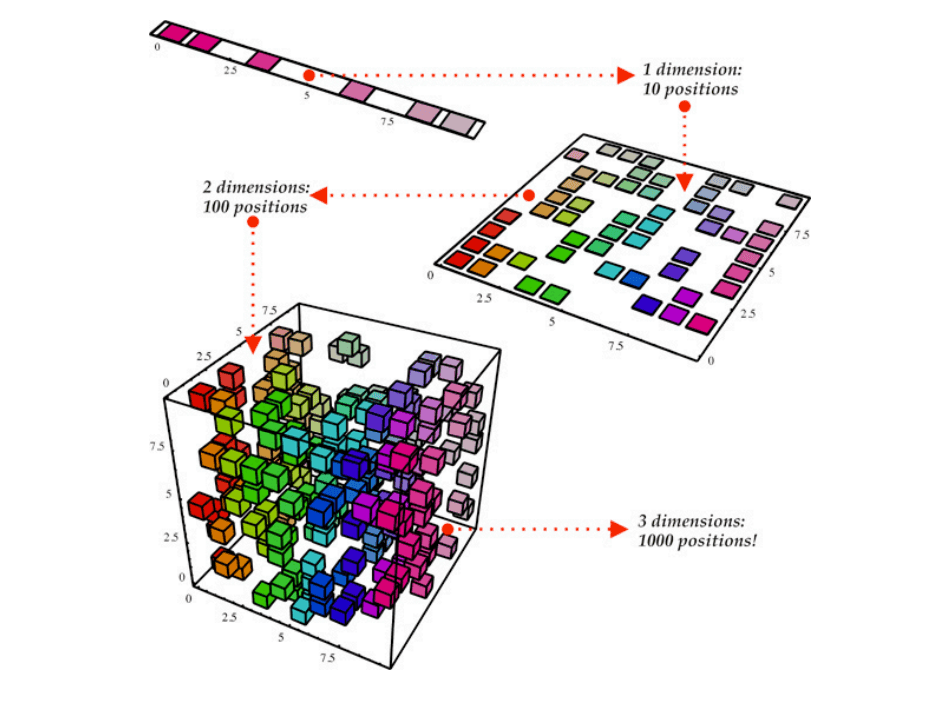
In Machine Learning, “dimensionality” refers to the number of features (i.e. input variables) in a dataset. These features (represented as columns in a tabular dataset) fed into a Machine Learning model are called predictors or “p”, and the samples (represented as rows) “n“. Most Machine Learning algorithms assume that there are many more samples than predictors. Still, sometimes the scenario is exactly the opposite, a situation referred to as “big-p, little-n” (“p” for predictors, and “n” for samples).
In industries like Life Sciences, data tends to behave exactly in this way. For example, by using high throughput screening technologies, you can measure thousands or millions of data points for a single sample (e.g., the entire genome, the amounts of metabolites, the composition of the microbiome). Why is this a problem? Because in high dimensions, the data assumptions needed for statistical testing are not met, and several problems arise:
- Data points move far away from each other in high dimensions.
- Data points move far away from the center in high dimensions.
- The distances between all pairs of data points become the same.
- The accuracy of any predictive model approaches 100%.
This situation is referred to as “the Curse of Dimensionality”, which states that as data dimensionality increases, we can suffer from a significant impact on the implementation time of certain algorithms, make visualization extremely challenging, and make some Machine Learning models useless. A large number of dimensions in the feature space can mean that the volume of that space is very large, and in turn, the points that we have in that space often represent a small and non-representative sample.
The good news is that we can reduce data dimensionality to overcome these problems. The concept behind dimensionality reduction is that high-dimensional data are dominated by a small number of simple variables. This way, we can find a subset of variables to represent the same level of information in the data or transform the variables into a new set of variables without losing much information.
Main Algorithms
When facing high-dimensional data, it is helpful to reduce dimensionality by projecting the data to a lower-dimensional subspace that captures the data’s “essence.” There are several different ways in which you can achieve this algorithmically: PCA, t-SNE and UMAP.
Principal Component Analysis (PCA)
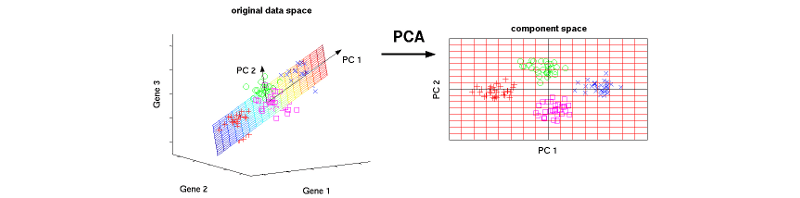
PCA is a linear dimensionality reduction algorithm that helps us extract a new set of variables from an existing high-dimensional dataset. The idea is to reduce the dimensionality of a dataset while retaining as much variance as possible.
PCA is also an unsupervised algorithm that creates linear combinations of the original features, called principal components. Principal components are learned in such a way that the first principal component explains maximum variance in the dataset, the second principal component tries to explain the remaining variance in the dataset while being uncorrelated to the first one, and so on.
Instead of simply choosing useful features and discarding others, PCA uses a linear combination of the existing features in the dataset and constructs new features that are an alternative representation of the original data.
This way, you might keep only as many principal components as needed to reach a cumulative explained variance of 85%. But why not keep all components? What happens is that each additional component expresses less variance and more noise, so representing the data with a smaller subset of principal components preserves the signal and discards the noise.
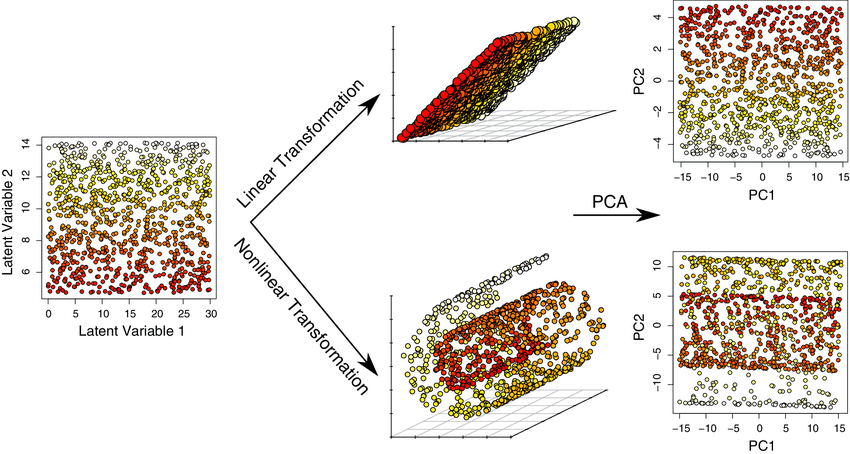
PCA increases interpretability while minimizing information loss. It can be used to find the most significant features in a dataset and allows data visualization in 2D and 3D. At the same time, PCA is most suitable when variables have a linear relationship among them (it won’t be able to capture more complex relationships) and is susceptible to significant outliers.
You can find a tutorial on calculating PCA in this link and an example coded in Python here.
t-Distributed Stochastic Neighbour Embedding (t-SNE)
Created for high-dimensional visualization purposes, t-SNE is a non-linear dimensionality reduction algorithm. This algorithm tries to maximize the probability that similar points are positioned near each other in a low-dimensional map while preserving longer-distance relationships as a secondary priority. It attracts data points that are nearest neighbors to each other and simultaneously pushes all points away from each other.
Contrary to PCA, t-SNE it’s not a deterministic technique but a probabilistic one. The idea behind it is to minimize the divergence between two distributions: a distribution that measures pairwise similarities of the input objects, and a distribution that measures pairwise similarities of the corresponding low-dimensional points in the embedding. It looks to match both distributions to determine how to best represent the original dataset using fewer dimensions.
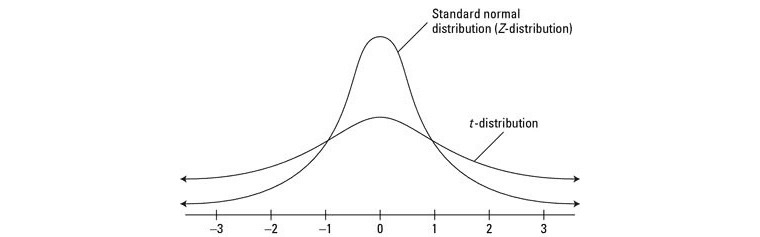
More specifically, t-SNE uses a normal distribution (in the higher dimension) and a t-Distribution (in the lower dimension) to reduce dimensionality. t-Distribution is a lot like a normal distribution, with the difference that it is not as tall as a normal distribution in the middle, but its tails are taller at the ends. The idea is to cluster data points in the lower dimension in a more sparse way to generate better visualizations.
There are several tuneable hyperparameters to optimize t-SNE, like:
- Perplexity, which controls the size of the neighborhood used for attracting data points.
- Exaggeration, which controls the magnitude of attraction.
- Learning rate, which controls the step size for the gradient descent that seeks to minimize the error.
Changing these hyperparameters can deeply affect the accuracy and quality of t-SNE results.
t-SNE is an incredibly flexible algorithm that can find structure where others cannot. Unfortunately, it can be hard to interpret: after processing, the input features are no longer identifiable, and you cannot make any inference based only on the outputs.
While being stochastic, multiple executions with different initializations will yield different results, and whatsmore, both its computational and memory complexity are O(n2 ), which can make it quite heavy on system resources.
Find here an interactive explanation of t-SNE.
Uniform Manifold Approximation and Projection (UMAP)
UMAP is another nonlinear dimension-reduction algorithm that overcomes some of the limitations of t-SNE. It works similarly to t-SNE in that it tries to find a low-dimensional representation that preserves relationships between neighbors in high-dimensional space, but with an increased speed and better preservation of the data’s global structure.
UMAP is a non-parametric algorithm that consists of two steps: (1) compute a fuzzy topological representation of a dataset, and (2) optimize the low dimensional representation to have as close a fuzzy topological representation as possible as measured by cross entropy.
There are two main hyperparameters in UMAP that are used to control the balance between local and global structure in the final projection:
- The number of nearest neighbors: which controls how UMAP balances local versus global structure - low values will push UMAP to focus more on the local structure by constraining the number of neighboring points considered when analyzing the data in high dimensions. In contrast, high values will push UMAP towards representing the big-picture structure, hence losing fine detail.
- The minimum distance between points in low-dimensional space: which controls how tightly UMAP clumps data points together, with low values leading to more tightly packed embeddings. Larger values will make UMAP pack points together more loosely, focusing instead on the preservation of the broad topological structure.
Fine-tuning these hyperparameters can be challenging, and this is where UMAP’s speed is a big advantage: by running it multiple times with a variety of hyperparameter values, you can get a better sense of how the projection is affected.
Compared to t-SNE, UMAP presents several advantages since it:
- Achieves comparable visualization performance with t-SNE.
- Preserves more of the global data structure. While the distance between the clusters formed in t-SNE does not have significant meaning, in UMAP the distance between clusters matters.
- UMAP is fast and can scale to Big Data.
- UMAP is not restricted for visualization-only purposes like t-SNE. It can serve as a general-purpose Dimensionality Reduction algorithm.
You can find an interactive explanation of UMAP here and try different algorithms and datasets in the TensorBoard Embedding Projector.
Why Reduce Dimensionality?
There’s one thing we can be certain about in Machine Learning: the future will bring more data. Whatsmore, Machine Learning models will continue to evolve to highly complex architectures. In that scenario, dimensionality reduction algorithms can bring huge benefits like:
- Reducing storage needs for massive datasets.
- Facilitating data visualizations by compressing information in fewer features.
- Making Machine Learning models more computationally efficient.
In turn, these benefits translate into better model performance, increased interpretability, and improved data scalability. But of course, dimensionality reduction comes with data loss. No dimensionality reduction technique is perfect : by definition, we’re distorting the data to fit it into lower dimensions. This is why it’s so critical to understand how these algorithms work and how they are used to effectively visualize and understand high-dimensional datasets.