Introduction
Vector embeddings are one of the most fascinating and useful concepts in machine learning. They are central to many NLP, recommendation, and search algorithms. If you’ve ever used things like recommendation engines, voice assistants, language translators, you’ve come across systems that rely on embeddings.
ML algorithms, like most software algorithms, need numbers to work with. Sometimes we have a dataset with columns of numeric values or values that can be translated into them (ordinal, categorical, etc). Other times we come across something more abstract like an entire document of text. We create vector embeddings, which are just lists of numbers, for data like this to perform various operations with them. A whole paragraph of text or any other object can be reduced to a vector. Even numerical data can be turned into vectors for easier operations.
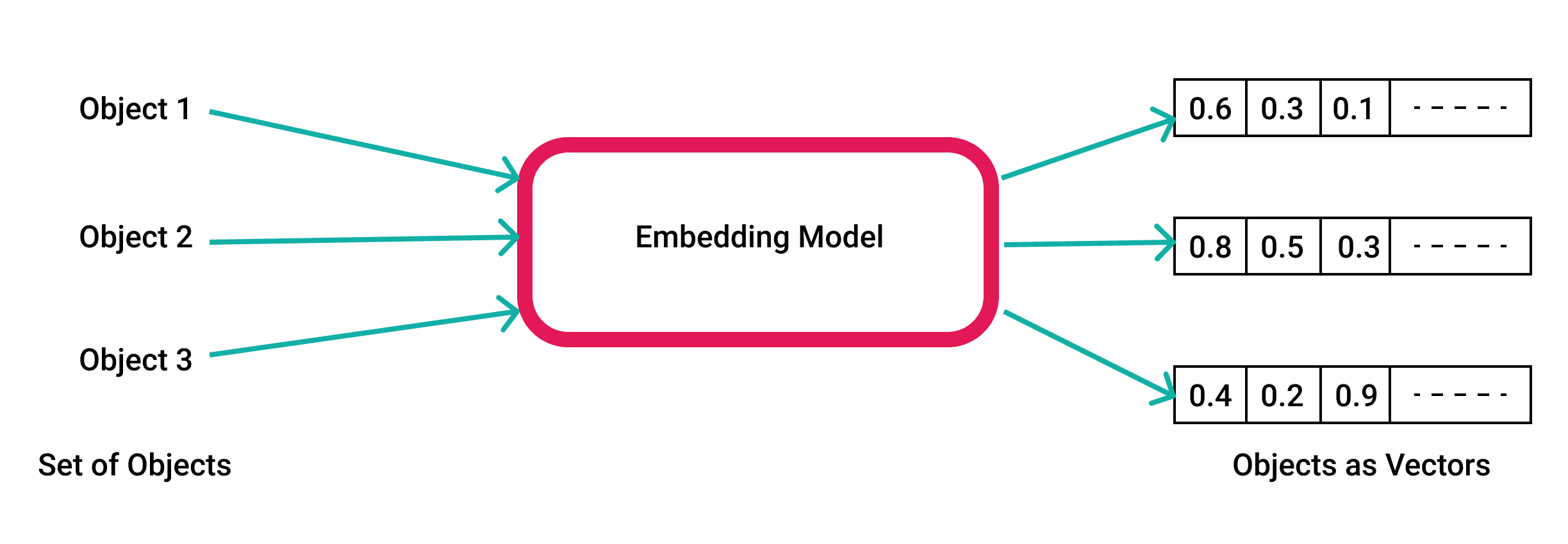
But there is something special about vectors that makes them so useful. This representation makes it possible to translate semantic similarity as perceived by humans to proximity in a vector space.
In other words, when we represent real-world objects and concepts such as images, audio recordings, news articles, user profiles, weather patterns, and political views as vector embeddings, the semantic similarity of these objects and concepts can be quantified by how close they are to each other as points in vector spaces. Vector embedding representations are thus suitable for common machine learning tasks such as clustering, recommendation, and classification.
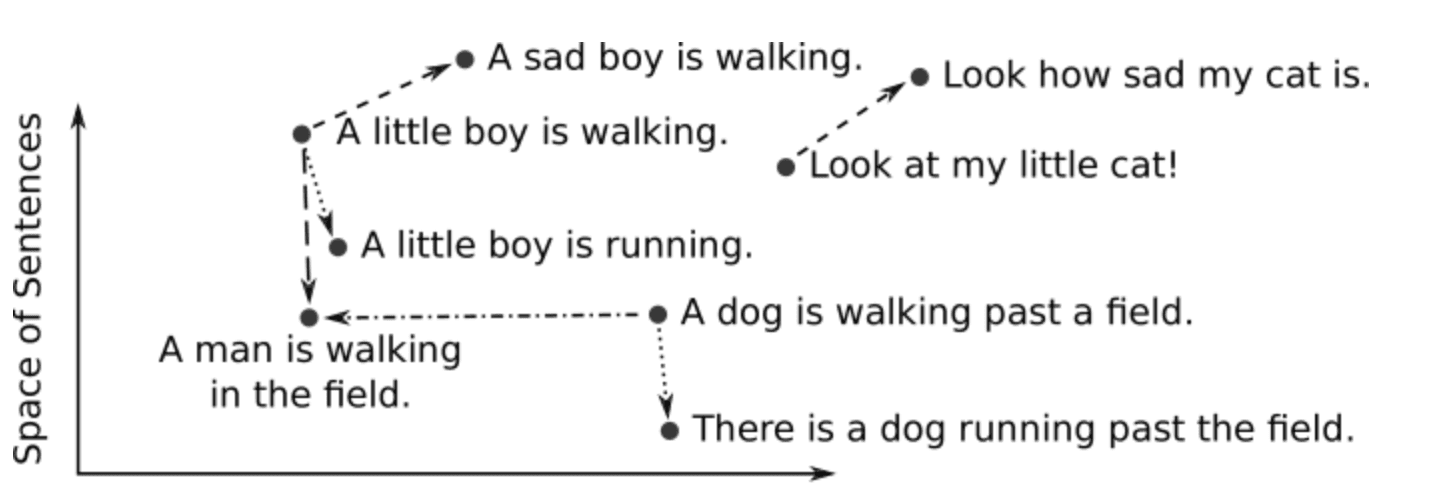
For example, in a clustering task, clustering algorithms assign similar points to the same cluster while keeping points from different clusters as dissimilar as possible. In a recommendation task, when making recommendations for an unseen object, the recommender system would look for objects that are most similar to the object in question, as measured by their similarity as vector embeddings. In a classification task, we classify the label of an unseen object by the major vote over labels of the most similar objects.
Creating Vector Embeddings
One way of creating vector embeddings is to engineer the vector values using domain knowledge. This is known as feature engineering. For example, in medical imaging, we use medical expertise to quantify a set of features such as shape, color, and regions in an image that capture the semantics. However, engineering vector embeddings requires domain knowledge, and it is too expensive to scale.
Instead of engineering vector embeddings, we often train models to translate objects to vectors. A deep neural network is a common tool for training such models. The resulting embeddings are usually high dimensional (up to two thousand dimensions) and dense (all values are non-zero). For text data, models such as Word2Vec, GLoVE, and BERT transform words, sentences, or paragraphs into vector embeddings.
Images can be embedded using models such as convolutional neural networks (CNNs), Examples of CNNs include VGG, and Inception. Audio recordings can be transformed into vectors using image embedding transformations over the audio frequencies visual representation (e.g., using its Spectrogram).
Example: Image Embedding with a Convolutional Neural Network
Consider the following example, in which raw images are represented as greyscale pixels. This is equivalent to a matrix (or table) of integer values in the range 0 to 255. Wherein the value 0 corresponds to a black color and 255 to white color. The image below depicts a greyscale image and its corresponding matrix.
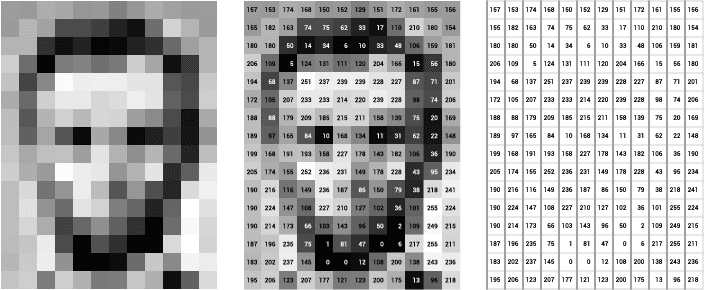
The left sub-image depicts the grayscale pixels, the middle sub-image contains the pixel grayscale values, and the rightmost sub-image defines the matrix. Notice the matrix values define a vector embedding in which its first coordinate is the matrix upper-left cell, then going left-to-right until the last coordinate which corresponds to the lower-right matrix cell.
Such embeddings are great at maintaining the semantic information of a pixel’s neighborhood in an image. However, they are very sensitive to transformations like shifts, scaling, cropping and other image manipulation operations. Therefore they are often used as raw inputs to learn more robust embeddings.
Convolutional Neural Network (CNN or ConvNet) is a class of deep learning architectures that are usually applied to visual data transforming images into embeddings.
CNNs are processing the input via hierarchical small local sub-inputs which are termed receptive fields. Each neuron in each network layer processes a specific receptive field from the former layer. Each layer either applies a convolution on the receptive field or reduces the input size, which is called subsampling.
The image below depicts a typical CNN structure. Notice the receptive fields, depicted as sub-squares in each layer, service as an input to a single neuron within the preceding layer. Notice also the subsampling operations reduce the layer size, while the convolution operations extend the layer size. The resulting vector embedding is received via a fully connected layer.
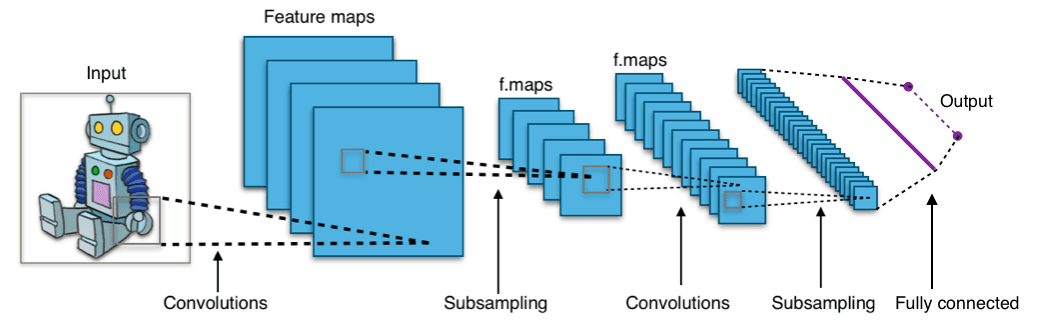
Learning the network weights (i.e., the embedding model) requires a large set of labeled images. The weights are being optimized in a way that images with the same labels are embedded closer compared to images with different labels. Once we learn the CNN embedding model we can transform the images into vectors and store them with a K-Nearest-Neighbor index. Now, given a new unseen image, we can transform it with the CNN model, retrieve its k-most similar vectors, and thus the corresponding similar images.
Although we used images and CNNs as examples, vector embeddings can be created for any kind of data and there are multiple models/methods that we can use to create them.
Using Vector Embeddings
The fact that embeddings can represent an object as a dense vector that contains its semantic information makes them very useful for a wide range of ML applications.
Similarity search is one of the most popular uses of vector embeddings. Search algorithms like KNN and ANN require us to calculate distance between vectors to determine similarity. Vector embeddings can be used to calculate these distances. Nearest neighbor search in turn can be used for tasks like de-duplication, recommendations, anomaly detection, reverse image search, etc.
Even if we don’t use embeddings directly for an application, many popular ML models and methods internally rely on them. For example in encoder-decoder architectures, embeddings produced by encoder contain the necessary information for the decoder to produce a result. This architecture is widely used in applications, such as machine translation and caption generation.
Check out some applications you can build with vector embeddings and Pinecone.
Was this article helpful?