Pinecone is a vector database that makes it easy to add similarity search to any application. Try it free, and continue reading to learn what makes similarity search so useful.
Introduction
Searching through data for similar items is a common operation in databases, search engines, and many other applications. Finding similar items based on fixed numeric criteria is very straightforward using a query language when we are dealing with traditional databases. For example, finding employees in a database within a fixed salary range.
But sometimes we have to answer questions like “Which objects in our inventory are similar to what a user searched for?” The search terms can be vague and can have a lot of variations. For example, a user can search for something generic like “shoes”,“black shoes” or something more precise like “Nike AF-1 LV8”.

Our system must be able to discern between these terms and must understand how a black shoe differs from other shoes. To handle such queries we need a representation that captures the deeper conceptual meaning of the objects. On top of that, in scenarios like these, we might have to work with data to the scale of billions of objects.
When dealing with data in this scale & context, this problem is quite unlike searching through traditional databases containing symbolic object representations. Hence we need something more powerful that can allow us to search through semantic representations efficiently.
With similarity search, we can work with semantic representations of our data and find similar items fast. And in the sections below we will discuss how exactly it works.
What Are Vector Representations?
In the passage above, we talked about representing objects in a way that captures their deeper meanings. In machine learning, we often represent real-world objects and concepts as a set of continuous numbers, also known as vector embeddings. This very neat method allows us to translate the similarity between objects as perceived by us into a vector space.
This means when we represent images or pieces of text as vector embeddings, their semantic similarity is represented by how close their vectors are in the vector space. Hence, what we want to look at is the distance between vectors of the objects.
These vector representations (embeddings) are often created by training models according to the input data and task. Word2Vec,GLoVE, USE etc. are popular models for generating embeddings from text data while CNN models like VGG are often used to create image embeddings.
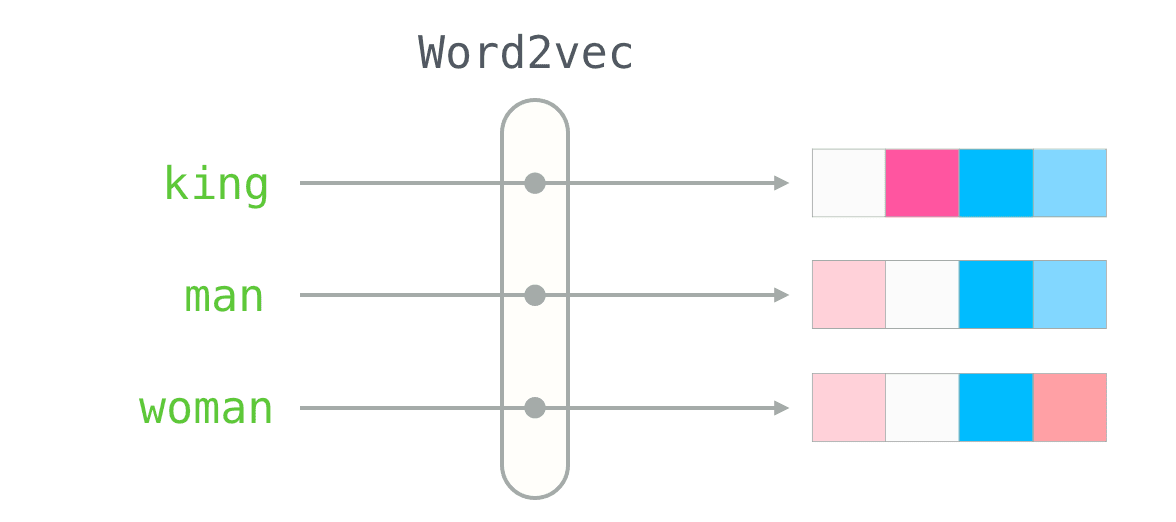
The figure above from this great article on word2vec, can help us visualize how the model can generate similar representations of similar words and is able to capture the semantic meaning.
This concept can be extended to more complex objects. We can combine information from features in the dataset to create embeddings for every row in the dataset. This is something leveraged by many search & recommendation based algorithms. The point that I want to make is, training a machine learning model on any data can transform the broad abstract concept it can have to something on which we can perform mathematical operations that can give us the insights we need.
Distance Between Vectors
We mentioned earlier that we find similarities between objects by calculating the distance between their vectors. We can calculate the distance between these vectors in the vectors space according to the distance metric that fits our problem the best.
Some of the commonly used distance metrics in ML are Euclidean, Manhattan, Cosine, and Chebyshev. The image below will help us understand the intuition behind each of these methods.
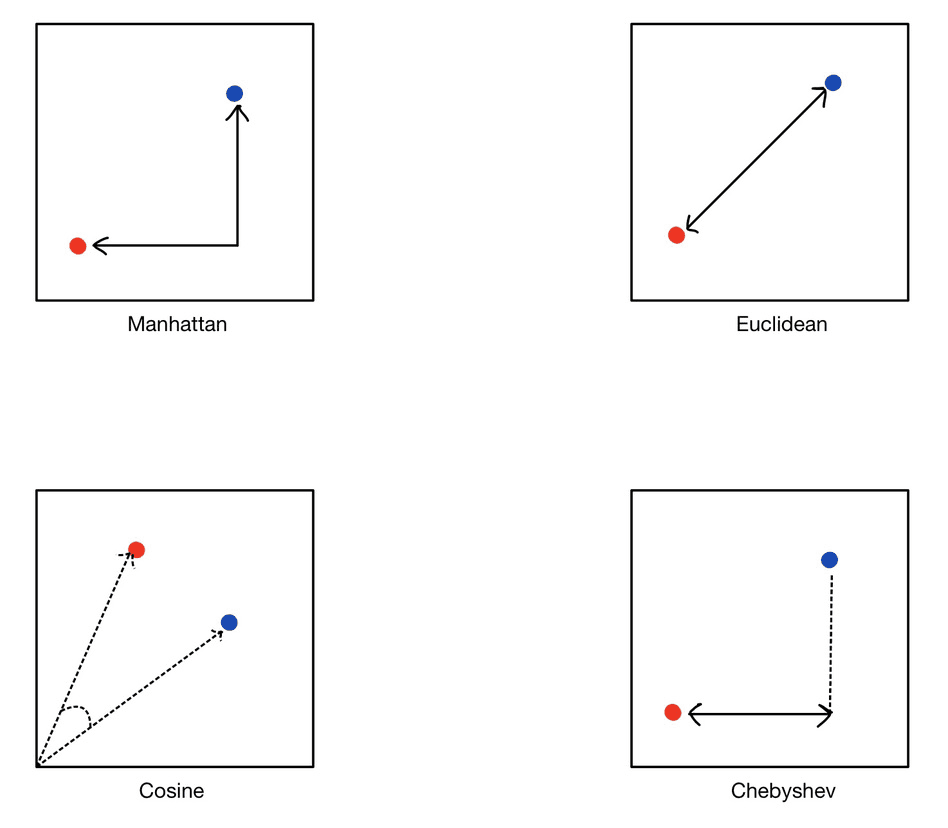
The choice of distance metric depends on the use case. A great guide to learn more about distance metrics is here.
Performing Search
Now we know we can use vector embeddings to represent our objects, and the distances between vectors represent the similarity between the objects themselves.
This is where the similarity search, or vector search, kicks in. Given a set of vectors and a query vector, we need to find the most similar items in our set for the query. We call this task nearest neighbor search.
K Nearest Neighbors
K nearest neighbors or k-NN is a very popular algorithm to find nearest vectors in a space for a given query vector. The k here is a hyperparameter set by us which denotes how many nearest neighbors we want to retrieve.
We can perform k-NN on the vectors we have for our data and retrieve the nearest neighbors for our query vector depending on the distance between the vectors.
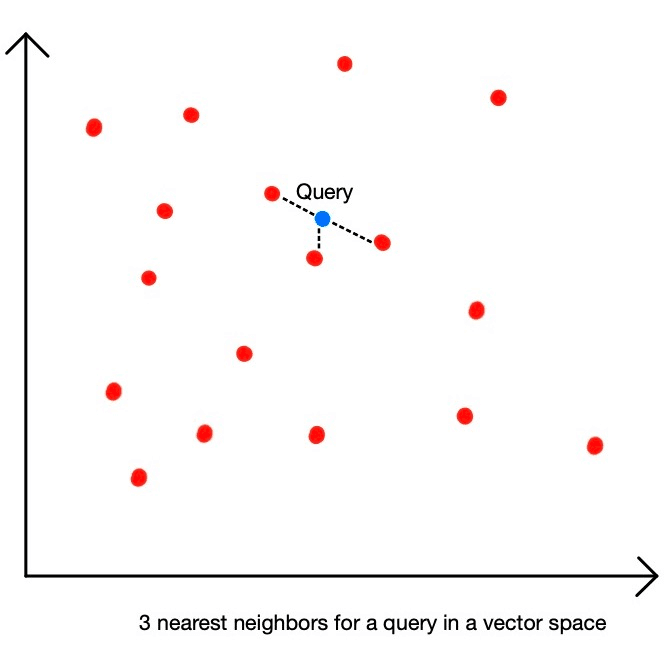
A major drawback of k-NN is that to find the nearest vectors for our query we will have to calculate its distance with every vector we have in our database. This will be very inefficient if we have to search through millions of vectors.
Approximate Neighbor Search
To reduce the computation complexity added by an exhaustive search like kNN we make use of approximate neighbor search.
Instead of checking distances between each vector in the database, we retrieve a “good guess” of the nearest neighbor. In some use cases, we would rather lose some accuracy in favor of performance gain, thus allowing us to scale our search. ANN allows us to get a massive performance boost on similarity search when dealing with huge datasets.
In approximately nearest neighbors (ANN), we build index structures that narrow down the search space and improve lookup times. Apart from that, most ML models produce vectors that have high dimensionality which is another hurdle to overcome. Approximate search relies on the fact that even though data is represented in a large number of dimensions, their actual complexity is low. It tries to work with the true intrinsic dimensionality of data. Hashing is a good example of a method that allows us to do it and is used widely for many applications. There are various algorithms to solve the approximate search problem and to actually dive into how approximate search works warrants another article of its own. I suggest going through this three-part series of articles to understand ANN better.
As an overview, it is sufficient to understand that ANN algorithms make use of techniques like indexing, clustering, hashing, and quantization to significantly improve computation and storage at the cost of some loss in accuracy.
Conclusion
While we have barely scratched the surface of the complexities of similarity search — also known as vector search — with this article, the intent was to introduce some basic concepts and provide resources for a detailed reading on the topic. An increasing number of applications make use of similarity search to untangle problems in search & other domains, I highly encourage diving deeper into some of these concepts to learn more!
While you are on the website, why not have a look at how easy it is to build a scalable similarity search system in just a few lines of code? You can find a few example notebooks that use Pinecone for solving similarity search and related problems. Grab your free API key and we will be happy to help you along the way!
Was this article helpful?