Build Better Deep Learning Models with Batch and Layer Normalization

Jun 23, 2023

Bala Priya C

Technical Writer

Recent advances in deep learning research have revolutionized fields like medical imaging, machine vision, and natural language processing. However, it’s still challenging for data scientists to choose the optimal model architecture and to tune hyperparameters for best results.

Even with the optimal model architecture, how the model is trained can make the difference between a phenomenal success or a scorching failure.

For example, take weight initialization: In the process of training a neural network, we initialize the weights which are then updated as the training proceeds. For a certain random initialization, the outputs from one or more of the intermediate layers can be abnormally large. This leads to instability in the training process, which means the network will not learn anything useful during training.

Batch and layer normalization are two strategies for training neural networks faster, without having to be overly cautious with initialization and other regularization techniques.

In this tutorial, we’ll go over the need for normalizing inputs to the neural network and then proceed to learn the techniques of batch and layer normalization.

Let’s get started!

Why Should You Normalize Inputs in a Neural Network?

When you train a neural network on a dataset, the numeric input features could take on values in potentially different ranges. For example, if you’re working with a dataset of student loans with the age of the student and the tuition as two input features, the two values are on totally different scales. While the age of a student will have a median value in the range 18 to 25 years, the tuition could take on values in the range $20K - $50K for a given academic year.

If you proceed to train your model on such datasets with input features on different scales, you’ll notice that the neural network takes significantly longer to train because the gradient descent algorithm takes longer to converge when the input features are not all on the same scale. Additionally, such high values can also propagate through the layers of the network leading to the accumulation of large error gradients that make the training process unstable, called the problem of exploding gradients.

To overcome the above-mentioned issues of longer training time and instability, you should consider preprocessing your input data ahead of training. Preprocessing techniques such as normalization and standardization transform the input data to be on the same scale.

Normalization vs Standardization

Normalization works by mapping all values of a feature to be in the range [0,1] using the transformation:

Suppose a particular input feature x has values in the range [x_min, x_max]. When x is equal to x_min, x_norm is equal to 0 and when x is equal to x_max, x_norm is equal to 1. So for all values of x between x_min and x_max, x_norm maps to a value between 0 and 1.

Standardization, on the other hand, transforms the input values such that they follow a distribution with zero mean and unit variance. Mathematically, the transformation on the data points in a distribution with mean μ and standard deviation σ is given by:

In practice, this process of standardization is also referred to as normalization (not to be confused with the normalization process discussed above). As part of the preprocessing step, you can add a layer that applies this transform to the input features so that they all have a similar distribution. In Keras, you can add a normalization layer that applies this transform to the input features.

Need for Batch Normalization

In the previous section, we learned how we can normalize the input to the neural network in order to speed up training. If you look at the neural network architecture, the input layer is not the only input layer. For a network with hidden layers, the output of layer k-1 serves as the input to layer k. If the inputs to a particular layer change drastically, we can again run into the problem of unstable gradients.

When working with large datasets, you’ll split the dataset into multiple batches and run the mini-batch gradient descent. The mini-batch gradient descent algorithm optimizes the parameters of the neural network by batchwise processing of the dataset, one batch at a time.

It’s also possible that the input distribution at a particular layer keeps changing across batches. The seminal paper titled Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift by Sergey Ioffe and Christian Szegedy refers to this change in distribution of the input to a particular layer across batches as internal covariate shift. For instance, if the distribution of data at the input of layer K keeps changing across batches, the network will take longer to train.

But why does this hamper the training process?

For each batch in the input dataset, the mini-batch gradient descent algorithm runs its updates. It updates the weights and biases (parameters) of the neural network so as to fit to the distribution seen at the input to the specific layer for the current batch.

Now that the network has learned to fit to the current distribution, if the distribution changes substantially for the next batch, it now has to update the parameters to fit to the new distribution. This slows down the training process.

However, if we transpose the idea of normalizing the inputs to the hidden layers in the network, we can potentially overcome the limitations imposed by exploding activations and fluctuating distributions at the layer’s input. Batch normalization helps us achieve this, one mini-batch at a time, to accelerate the training process.

What is Batch Normalization?

For any hidden layer h, we pass the inputs through a non-linear activation to get the output. For every neuron (activation) in a particular layer, we can force the pre-activations to have zero mean and unit standard deviation. This can be achieved by subtracting the mean from each of the input features across the mini-batch and dividing by the standard deviation.

Following the output of the layer k-1, we can add a layer that performs this normalization operation across the mini-batch so that the pre-activations at layer k are unit Gaussians. The figure below illustrates this.

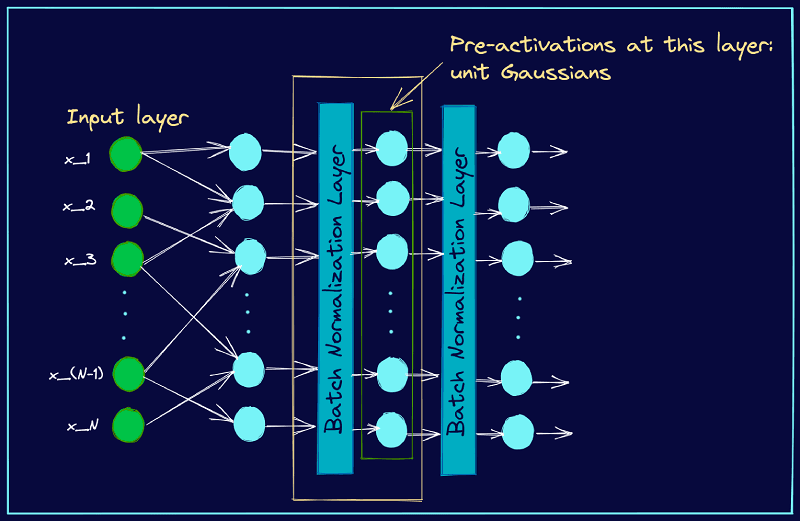
Section of a Neural Network with Batch Normalization Layer (Image by the author)

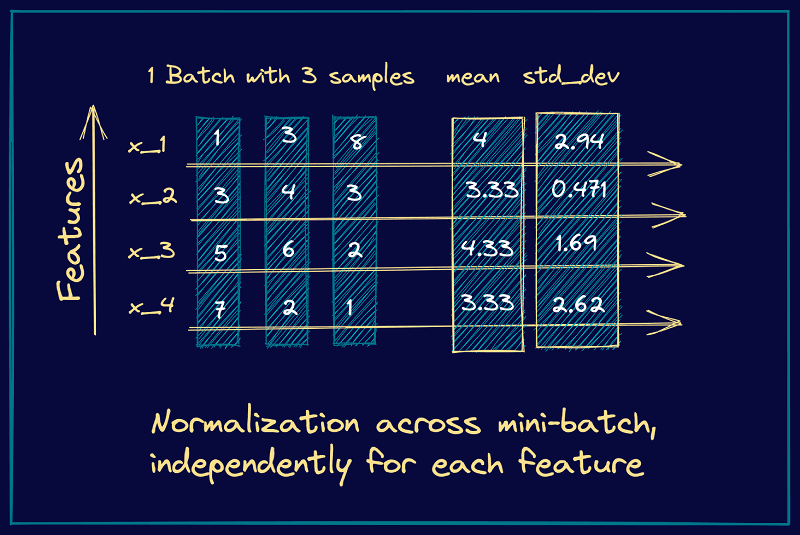
As an example, let’s consider a mini-batch with 3 input samples, each input vector being four features long. Here’s a simple illustration of how the mean and standard deviation are computed in this case. Once we compute the mean and standard deviation, we can subtract the mean and divide by the standard deviation.

How Batch Normalization Works - An Example (Image by the author)

However, forcing all the pre-activations to be zero and unit standard deviation across all batches can be too restrictive. It may be the case that the fluctuant distributions are necessary for the network to learn certain classes better.

To address this, batch normalization introduces two parameters: a scaling factor gamma (γ) and an offset beta (β). These are learnable parameters, so if the fluctuation in input distribution is necessary for the neural network to learn a certain class better, then the network learns the optimal values of gamma and beta for each mini-batch. The gamma and beta are learnable such that it’s possible to go back from the normalized pre-activations to the actual distributions that the pre-activations follow.

Putting it all together, we have the following steps for batch normalization. If x(k) is the pre-activation corresponding to the k-th neuron in a layer, we denote it by x to simplify notation.

Limitations of Batch Normalization

Two limitations of batch normalization can arise:

In batch normalization, we use the batch statistics: the mean and standard deviation corresponding to the current mini-batch. However, when the batch size is small, the sample mean and sample standard deviation are not representative enough of the actual distribution and the network cannot learn anything meaningful.
As batch normalization depends on batch statistics for normalization, it is less suited for sequence models. This is because, in sequence models, we may have sequences of potentially different lengths and smaller batch sizes corresponding to longer sequences.

Later, we’ll examine layer normalization, another technique that can be used for sequence models. For convolutional neural networks (ConvNets), batch normalization is still recommended for faster training.

How to Add a Batch Normalization Layer in Keras

Keras provides a BatchNormalization class that lets you add a batch normalization layer wherever needed in the model architecture. For a complete review of the different parameters you can use to customize the batch normalization layer, refer to the Keras docs for BatchNormalization.

The code snippet below shows how you can add batch normalization layers to an arbitrary sequential model in Keras. You can choose to selectively apply batch normalization to specific layers in the network.

import keras

from keras.models import Sequential
from keras.layers import Dense, Activation, BatchNormalization

model = Sequential([
    Dense(units=10, input_shape=(1,4), activation='relu'),
    # add batchnorm layer after activations in the previous layer
    BatchNormalization(axis=1),
    # pre-activations at the dense layer below are Gaussians
    Dense(units=16, activation='relu'),
    BatchNormalization(axis=1),
    Dense(units=4, activation='softmax')
])

It’s important to understand how batch normalization works under the hood during training and testing. During training, batch normalization computes the mean and standard deviation corresponding to the mini-batch.

However, at test time (inference time), we may not necessarily have a batch to compute the batch mean and variance. To overcome this limitation, the model works by maintaining a moving average of the mean and variance at training time, called the moving mean and moving variance. These values are accumulated across batches at training time and used as mean and variance at inference time.

What is Layer Normalization?

Layer Normalization was proposed by researchers Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E. Hinton. In layer normalization, all neurons in a particular layer effectively have the same distribution across all features for a given input.

For example, if each input has d features, it’s a d-dimensional vector. If there are B elements in a batch, the normalization is done along the length of the d-dimensional vector and not across the batch of size B.

Normalizing across all features but for each of the inputs to a specific layer removes the dependence on batches. This makes layer normalization well suited for sequence models such as transformers and recurrent neural networks (RNNs) that were popular in the pre-transformer era.

Here’s an example showing the computation of the mean and variance for layer normalization. We consider the example of a mini-batch containing three input samples, each with four features.

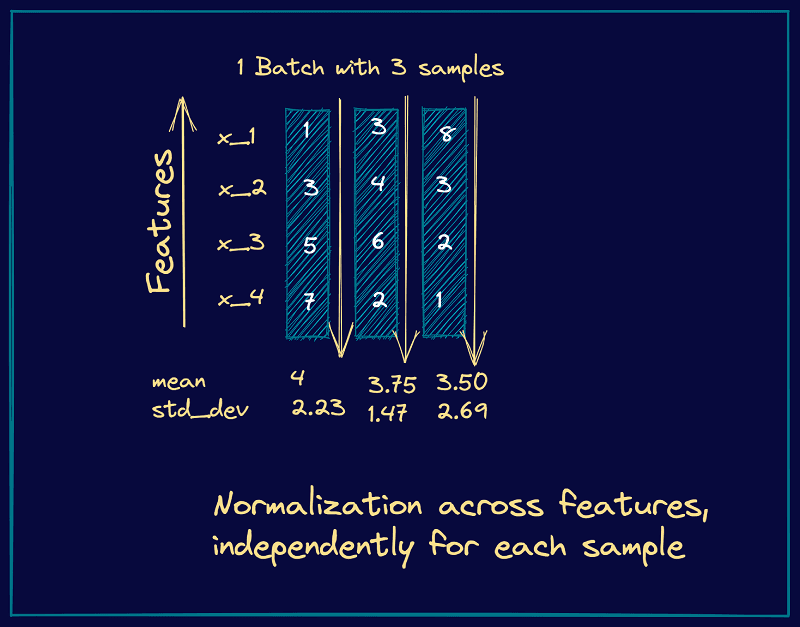
How Layer Normalization Works - An Example (Image by the author)

From these steps, we see that they’re similar to the steps we had in batch normalization. However, instead of the batch statistics, we use the mean and variance corresponding to specific input to the neurons in a particular layer, say k. This is equivalent to normalizing the output vector from the layer k-1.

How to Add a Layer Normalization in Keras

Similar to batch normalization, Keras also provides a LayerNormalization class that you can use to add layer normalization to the inputs of specific layers. The code cell below shows how you can add layer normalization in a simple sequential model. The parameter axis specifies the axis along which the normalization should be done.

import keras

from keras.models import Sequential
from keras.layers import Dense, Activation, LayerNormalization

model = Sequential([
    Dense(units=16, input_shape=(1,10), activation='relu'),
    LayerNormalization(axis=1),
    Dense(units=10, activation='relu'),
    LayerNormalization(axis=1),
    Dense(units=3, activation='softmax')
])

To understand how layer normalization is used in transformers, consider reading this TensorFlow tutorial on transformer models for language understanding.

Batch Normalization vs Layer Normalization

So far, we learned how batch and layer normalization work. Let’s summarize the key differences between the two techniques.

Batch normalization normalizes each feature independently across the mini-batch. Layer normalization normalizes each of the inputs in the batch independently across all features.
As batch normalization is dependent on batch size, it’s not effective for small batch sizes. Layer normalization is independent of the batch size, so it can be applied to batches with smaller sizes as well.
Batch normalization requires different processing at training and inference times. As layer normalization is done along the length of input to a specific layer, the same set of operations can be used at both training and inference times.

Final Thoughts

In this tutorial, you learned the basics of and differences between batch and layer normalization techniques and how to implement them in Keras.

Over the past several years, batch normalization and layer normalization have emerged as the go-to normalization techniques in computer vision and natural language processing, respectively. In certain computer vision tasks, group and instance normalization are also used. For further reading, consider checking out the recommended resources in the section below. Happy learning!